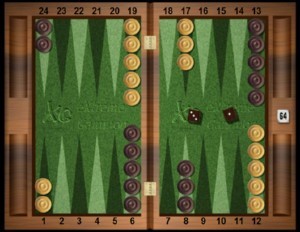
The word blunder is conventionally used in backgammon to indicate a checker play or cube action mistake which costs 0,100 or more in equity.  What does this mean?

Equity

Those of us who use eXtremeGammon as a learning tool are familiar with the numbers used in computer analysis.  People not familiar with computer analysis, however,  probably have no idea what  these numbers are about.  Still, it may be useful to have at least an idea of what the numbers reflect.

At the beginning of a game, the equity of both players is zero, which means that  none of the players has even the slightest advantage over the other.  If you win the game your equity has become +1.  The loser of the game then has an equity of – 1.  During the game the player who is favourite to win the game will have a positive equity of something between 0 and 1, whereas the underdog will have the same equity, but negative.

Let us have a look at an example.  Mind you : we are playing a 1-point match here, so gammons do not count and are not taken into the mix.

Once again, it should be clear to every reader that at the beginning of this 1-point match, the probability of winning the match for either player is 50% or fifty-fifty (if both players are of equal playing strength).  The equity of both players is 0 ( = zero).

1.  8/5 6/5 eq:+0,100
Player: 55,00%

We see that by winning the opening roll and finding the strongest possible opening roll, 31, Black is suddenly favourite to win the game.  He has 55% winning chances (it is actually slightly more, but I have rounded down a bit).  His equity has gone up from zero to +0,100.

Where does that + 0,100 come from?  Well, it reflects the difference between the winning percentage of the favourite (55%) and the winning percentage of the underdog (45%), which is 10%.  10% of 1 = 0,100.

If, however, you misplay your 31 and play the second best move, 13/10 6/5, you have gained no advantage.  Your winning chances are still 50% (actually it is a bit lower) and your equity is still zero (because your opponent is now on roll).

2. 13/10 6/5 eq: 0
Player: 50%

The bot tells us that playing 13/10 6/5 costs 0,100 in equity (the difference between 55% and 50%) :

2. 13/10 6/5 eq: 0 (-0,100)
Player: 50%

We have made a blunder.

Since not all blunders cost exactly 0,100 in equity, they are quantified in millipoints (one millipoint  of course being one thousandth of a point).  Here we would say that the player made a 100 millipoint blunder.

In the bag.

To help get a feel for the magnitude of this blunder, let us visualize a bag with 500 black and 500 red casino chips.  The black ones are yours and they have a value of + 1€.  The red ones have a value of -1€.

It is clear that with 500 black and 500 red chips in the bag, the value of the bag (i.e. your equity) is zero.  If you replace all the red chips by black chips, there will be 1,000 black chips in the bag and no red chips, so the value of the bag becomes 1,000€ (i.e. your equity is + 1,000).

If you replace 50 red chips by 50 black chips, there will be 550  black chips in the bag and 450 red chips.  The value of the bag has become : + 550 – 450 = 100€.  Your equity is no longer zero, but + 100.

Look at it this way : if your life depended on drawing a black chip from the bag, would you grab a chip from the bag with 500 black chips and 500 red chips, or would you feel slightly more comfortable drawing one from the bag with 550 black chips and 450 red chips?

If you think this difference is negligible, then I suggest you quit playing backgammon and start gardening.

The difference is substantial.  It is the difference between 55% chance of survival and 50% chance of survival.  This is huge. So, in backgammon terms,  picking a chip from the bag with only 500 black chips would be a  blunder, namely the difference in equity between 0 and 100.

Exercises.

1) After 10 moves in your backgammon game, your winning chances have gone up to 65%.  What is your equity?

O + 0,150

O + 0,300

0 + 0, 650

2) You have a choice between two moves.  One move gives you 80% winning chances and the other gives you only 70% winning chances.  How big is the blunder if you make the wrong move?

O 200 millipoints or -0,200

O 100 millipoints or – 0,100

0 400 millipoints or – 0,400

3) The game is not going your way.  The probability of you winning the game has gone down to 30%.  What is your equity?

O – 0,200

O – 0,400

O – 0,300

4) What is Black’s equity here if he is on roll?

 

O +0,250

O +0,750

O +0,500

5) Your equity in a DMP-game is +0,340.  How much wc do you have? Or, in other words, what is your winning%?

O 66%

O 34%

O 67%

Answers

1) With 650 black chips in the bag and 350 red chips, the value of the bag would be +650 – 350 = 300€.  Therefore your equity is +0,300.

2) With 80% wc (= winning chances) your equity would be + 0,600 (800-200).  With 70% wc your equity would be : 700 – 300 = 400, so : 0,400.  Your blunder is a double whopper, costing 200 millipoints or 0,200.

3) If you have 30% wc, your opponent has 70% wc.  The difference is 40%.  So your equity is – 0,400.

4) Every intermediate player should know that Black wins this game unless he rolls one of 9 rolls out of 36.  These rolls are : 11, 21, 31, 41 and 32.  So he has 75% wc.  His equity therefore is +0,500.

5) Easy : 340 divided by 2 is 170.  If you add that to 50 you have your wc.  Answer : 67%.  Once again, your equity is the difference between the winning% of the favourite and the winning% of the underdog : 67 – 33 = 34.  In millipoints this becomes 0,340.

M